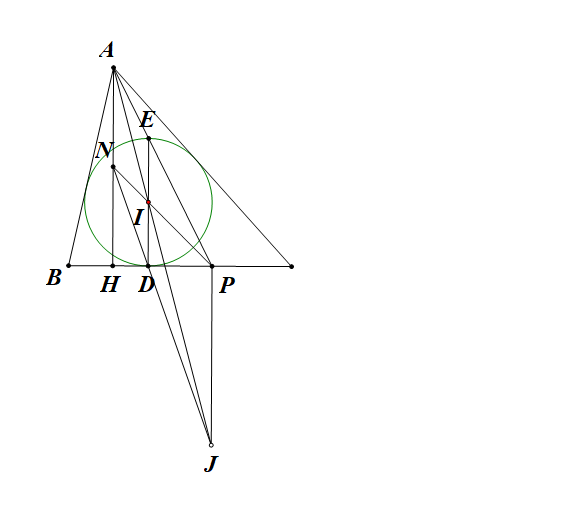Gọi \(BI,CI\) cắt \(EF\) tại lần lượt \(P,Q\). Ta có kết quả quen thuộc rằng: \(BP,CQ\) là các đường cao của tam giác \(IBC\) dẫn đến ta đổi mô hình về bài toán sau:

Cho tam giác \(HBC\) có trực tâm \(I\). \(M\) là hình chiếu của \(I\) lên \(PQ\). Kẻ đường cao \(DK\) của tam giác \(DPQ\). Chứng minh rằng: \(HM\) chia đôi \(DK\). 

Gọi \(PQ\cap BC=S\). Chú ý rằng: \( (SD,BC)=1\). Ta có: \(M(IH,DK)=M(HI,KD)=P(SD,BC)=-1\). Do đó: \(MH\) chia đôi \(DK\).

Gọi U,V lần lượt là giao điểm của BI, CI với EF. 

Tính chất quen thuộc: CV \(\perp\) KB tại V và BU \(\perp\) KC tại U

\(\rightarrow\) I là trực tâm của \(\Delta\)KBC \(\rightarrow\) I là tâm nội tiếp của \(\Delta\)DUV 

và K là tâm bàng tiếp wrt D của tam giác 

Ta đưa về một bài toán quen thuộc: Cho tam giác ABC có đường tròn nội tiếp (I) tiếp xúc với BC tại D 

và đường tròn bàng tiếp wrt A tiếp xúc với BC tại P. Gọi H là hình chiếu của A lên BC và N là trung điểm

của AH. Chứng minh rằng J,D,N thẳng hàng.

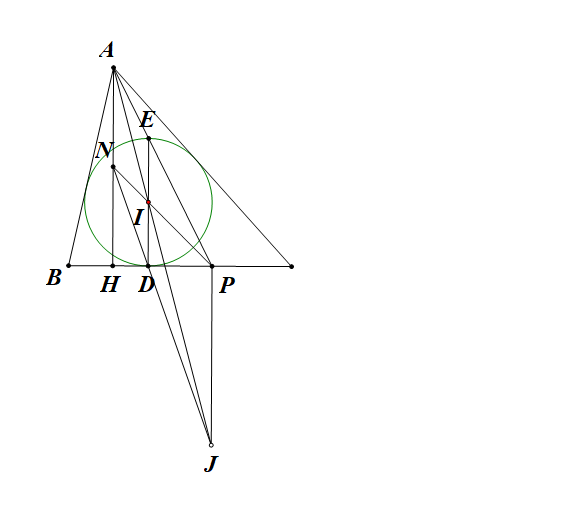
Dựng đường kính DE. Quen thuộc: A,E,P thẳng hàng

\(\rightarrow\)P,I,N thẳng hàng

Ta có: PJ//AN,NH// DI và NH=AN \(\rightarrow\) \(\frac{AN}{JP}\)=\(\frac{NI}{IP}\)=\(\frac{NH}{PJ}\)=\(\frac{HD}{DP}\)

\(\rightarrow\)J,D,N thẳng hàng

Áp dụng vào bài toán thì ta có đpcm