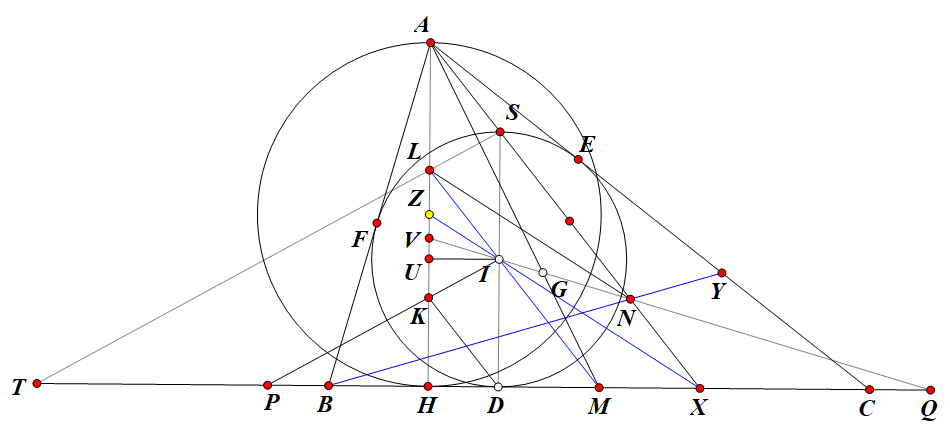
Gọi \(X, Y, Z\) là trung điểm \(BC, CA, AB\), \(D, E, F\) là tiếp điểm của \( (I) \) với \(BC, CA, AB\). Gọi \(H\) là trực tâm \(\triangle IBC\), khi đó \(H\) là cực của \(YZ\). Có một nhận xét là \(DFe, EF, YZ\) đồng quy tại một điểm \(K\). Có \(A\) là cực của \(EF\), \(YZ\) là cực của \(H\), \(DFe\) là cực của \(P\) nên \(A, H, P\) thẳng hàng. Điều cần chứng minh tương đương với việc chứng minh \(G\) là trọng tâm \(\triangle AQP\), vậy chỉ cần chứng minh \(IG\) chia đôi \(AP\) là xong, tức là chứng minh \(IG\) đi qua giao điểm \(T = AP \cap YZ\) là ổn. Thật vậy, \(XY\) là đối cực của \(H\) nên \(T\) và \(H\) liên hợp; \(AP\) là đối cực của \(K\) nên \(T\) và \(K\) cũng liên hợp, suy ra \(HK\) là đối cực của \(T\), tức là \(IT \perp HK \), thế nên giờ chứng minh được \(IG \perp HK\) là xong. Gọi \(U\) là giao điểm của đường thẳng qua \(C\) song song với \(BC\) với \(DE\), tương tự là điểm \(V\) với đỉnh \(B\). Ta có nhận xét là \(IF, CZ, DE\) đồng quy tại \(R\). Đối cực của \(C\) là \(DE\) nên \(U\), \(C\) liên hợp, và \(R\), \(C\) cũng liên hợp. Mà lại có \(CU \perp IR\) nên \(CU\) là đối cực của \(R\), suy ra \(U, R\) liên hợp, kết hợp với \(U, C\) liên hợp, suy ra \(CR\), hay \(CZ\), chính là đối cực của \(U\). Ta có nhận xét \(CZ, YZ, FZ\) lần lượt là đối cực của \(U, H, F\) nên ba điểm này thẳng hàng, tương tự ta có \(V, H, E\) thẳng hàng. Ta đã chứng minh \(U\) là cực của \(CZ\), suy ra \(U, G\) liên hợp, tương tự \(V, G\) liên hợp, suy ra \(IG \perp UV\). Vậy ta chỉ cần chứng minh \(UV \parallel HK\) là xong. Gọi \(J = AH \cap EF\) thì \( H(KA;UV) = H(KJ; EF) = (KJ; EF) = -1\) do \(AP\) là đối cực của \(K\), vậy ta cần chứng minh \(AH\) chia đôi \(UV\). Thật vậy, gọi \( A_b, A_c\) là giao của đường thẳng qua \(A\) song song \(BC\) với \(DE, DF\). Gọi \(A_1, A_2\) là giao điểm của cách cặp cạnh \(DF \cap AC, DE \cap AB\). Khi đó ta có \(A\) là trung điểm \(A_1A_2\). Ta chứng minh \(AH\) chia đôi \(A_1A_2\). Có nhận xét là \(\frac{S_{\triangle HDB}}{S_{\triangle HA_2B}} = 1 \) do \( A_2D \parallel HB\). Vậy ta có \(\frac{S_{\triangle AHA_2}}{S_{\triangle AHA_1}} = \frac{S_{\triangle AHA_2}}{S_{\triangle BHA_2}} .\frac{S_{\triangle BHA_2}}{S_{\triangle CHA_1}}. \frac{S_{\triangle CHA_1}}{S_{\triangle AHA_1}} = \frac{A_2B}{A_2A}.\frac{S_{\triangle DHB}}{S_{\triangle DHC}}.\frac{A_1A}{A_1C} = \frac{FB}{FA}.\frac{DC}{DB}.\frac{EA}{EC} = 1\), vậy \(AH\) chia đôi \(A_1A_2\). Gọi \(B_1, C_1\) lần lượt là đối xứng của \(C, B\) qua trung điểm \(AB, AC\). Khi đó ta có biến đổi tỉ số: \( \frac{\overline{VA_c}}{\overline{UA_b}} = \frac{\overline{VA_c}}{\overline{DA_1}}.\frac{\overline{DA_1}}{\overline{DA_2}}.\frac{\overline{DA_2}}{\overline{UA_b}} = \frac{\overline{A_cB_1}}{\overline{CD}}.\frac{\overline{DA_1}}{\overline{DA_2}}.\frac{\overline{BD}}{\overline{C_1A_b}} = \frac{\overline{DA_1}}{\overline{DA_2}}.\frac{\overline{DB}}{\overline{DC}} = \frac{\overline{A_1D}}{\overline{A_1F}}.\frac{\overline{A_1F}}{\overline{A_1V}}.\frac{\overline{A_1V}}{\overline{A_2U}}.\frac{\overline{A_2U}}{\overline{A_2E}}.\frac{\overline{A_2E}}{\overline{A_2D}}.\frac{\overline{DB}}{\overline{DC}} \)

\(= \frac{\overline{CD}}{\overline{CB}}.\frac{\overline{AB}}{\overline{AF}}.\frac{\overline{AF}}{\overline{AB}}.\frac{\overline{A_1V}}{\overline{A_2U}}.\frac{\overline{AC}}{\overline{AE}}.\frac{\overline{AE}}{\overline{AC}}.\frac{\overline{BC}}{\overline{BD}} = \frac{\overline{A_1V}}{\overline{A_2U}}\), suy ra trung điểm \(A_bA_c, UV, A_1A_2 \) thẳng hàng theo ERIQ, tức là \(AH\) chia đôi  \(UV\), ta có điều cần chứng minh.

Ta sẽ chứng minh rằng: \(I(xM,QP)=-1\) với \(Ix\|BC\). 
Chiếu xuyên tâm ta có: \(I(xM,QP)=-1=I(UL,VK)\).

Theo cách xác định điểm \(Feuerbach\) thì: \(S,L,F_e\) thẳng hàng. Như vậy hoàn toàn có thể bỏ qua điểm \(Feuerbach\) bởi ta đã có: \(IK\| SL\).

Do đó: \(L\) là trung điểm của \(AK\). Ta có: \(\dfrac{LK}{LV}=\dfrac{LA}{LV}=\dfrac{IN}{IV}\)(do \(MI\| AS\)) như vậy cần có: \(KN\| BC\) là kết thúc chứng minh. Ta có: \(IX\) chia đôi đường cao qua \(A\).

Như vậy ta cần chỉ ra rằng: \(LN\| ZX\). Điều này tương đương: \(\dfrac{AL}{AZ}=\dfrac{AN}{AX}\) hay \(\dfrac{2r}{h_a}=\dfrac{AN}{AX}\). Như vậy còn lại là 1 đoạn tính toán với các cạnh của tam giác \(ABC\), các bạn tự chơi nốt nhé :))